HackNotts ‘25 was a fantastic event. The largest iteration of the best (I’m totally unbiased) hackathon in the country! My first hackathon in a very long time where I worked on my own. I’m glad I did for this one, as I’m not sure that I’d have been able to convince any of my friends to work on this project.

Music and Functional Programming

There was a paper not long ago at ICFP ‘25 by Youyou Cong titled Continuations in Music. She spoke about the link between continuations, a powerful concept in functional programming, and patterns and structures in music.

I found this really interesting and wondered how far we might be able to take it!

The SK combinator calculus

Believe it or not, we can define a language using just two symbols which is as powerful as the lambda calculus. Defined by reduction rules. (Using ., non-standardly, to denote application. Lowercase letters are meta-variables and not part of the calculus.)

S . f . g . x = (f . x) . (g . x)
K . x . y = x

Surprisingly we can do a lot in this language. We can’t listen to it though.

The MUSIK combinator calculus

Let’s combine music and calculus!

Notes and sequences

Music consists of two dimensional sequences. Melodies are horizontal and chords are vertical.

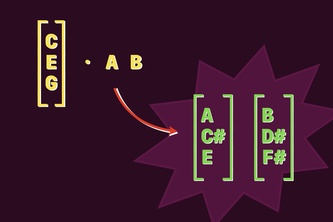
I decided that the primitives in my calculus shouldn’t be individual symbols, but should instead be sequences, of the two-dimensional sort. We represent these by syntactic juxtaposition, and use square brackets for verticals.

MUSIK> C C G G A A G
C C G G A A G

MUSIK> [(C C) [C E G]] [(G G) [G C]] (A A) [C E G]

┌   ┐ ┌   ┐
│C C│ │G G│       ┌ ┐
│┌ ┐│ │┌ ┐│       │C│
││C││ ││G││ (A A) │E│
││E││ ││C││       │G│
││G││ │└ ┘│       └ ┘
│└ ┘│ └   ┘
└   ┘

We hear horizontal sequences as rows, and verticals are played as chords. These compose and nest nicely, and behave as expected.

The M U and I combinators

We have new data, we ought to have new combinators to deal with them. We need three, as it happens.

M . c . n . ()     = n
M . c . n . (x y ...) = c . x . (M . c . n . (y ...))

U . (x y ...) . (a b ...) = (x y ... a b ...)
U . [x y ...] . (a b ...) = [x y ... a b ...]

I . p . s . z . C = z
I . p . s . z . i = s . (I . p . s . z . (i-1))     if i > 0
I . p . s . z . i = p . (I . p . s . z . (i+1))     if i < 0

M and I stand for “catamorphism” and “interval”, and U for “union”. M and I let us fold over the structure of sequences and intervals (i.e. notes). U lets us concatenate together sequences. By the way, U also gives us the power to transpose them.

Notes are combinators too

It only makes sense that we can use notes and musical passages as combinators too! They act as shifting operations, resp. their interval relative to middle C.

MUSIK> C# . [A B C]

     ┌ ┐
     │A│
C# · │B│
     │C│
     └ ┘

  ... 4 steps ...

┌  ┐
│A#│
│C5│
│C#│
└  ┘

This is interesting in itself, but it lets us do cool things like converting sequences into sequences of chords, or arpeggiating.

MUSIK> [C E G] . (A B)

┌ ┐
│C│
│E│ · A B
│G│
└ ┘

  ... 9 steps ...

┌   ┐ ┌   ┐
│ A │ │ B │
│C#5│ │D#5│
│ E5│ │F#5│
└   ┘ └   ┘

MUSIK> (C E G) . (C C G G A A G G F F E E D D C C)

C E G · C C G G A A G G F F E E D D C C

  ... 65 steps ...

(C E G) (C E G) (G B D5) (G B D5) (A C#5 E5) (A C#5 E5) (G B D5) (G B D5) (F A C5) (F A C5) (E G# B) (E G# B) (D F# A) (D F# A) (C E G) (C E G)

Operations on, and within, music

Music therefore can be seen simultaneously as data and code. For one example, we can use the I combinator to create a musical passage I . C# . Cb . C which inverts another.

MUSIK> (I . C# . Cb . C) . (C D E)

I · C# · B3 · C · C D E

  ... 16 steps ...

C A#3 G#3

We might also want to reverse a sequence. No worries, we can do this with the M and U operators.

MUSIK> M . (\a -> \rest -> U . rest . a) . () . (C E G)

M · (S · (K · (S · (S · (K · U) · (S · K · K)))) · (S · (K · K) · (S · K · K))) · () · C E G

  ... 43 steps ...

((() G) E) C

Hold on, lambdas?

Don’t worry, the calculus is still variable-free and entirey symbolic! I’m just using the standard lambda calculus to SK conversion, generalised to the MUSIK combinators.

This lets us write larger functions in a more intuitive and readable way. You can see above how the reverse function is mapped into purely the combinators in the language.

Sound

Terms in this language can be interpreted by playing them through a MIDI synth. It sounds pretty funky sometimes.